Идеальные элементы моделирующие работу операционного усилителя

 

АНОМАЛЬНЫЕ ЭЛЕМЕНТЫ

В ряде случаев анализ и синтез цепей с операционными усилителями, а также с полупроводниковыми триодами и электронными лампами, существенно упрощаются, если воспользоваться аномальными (патологическими) элемента­ми, к которым относятся нуллатор, норатор, нуллор и бигенератор.

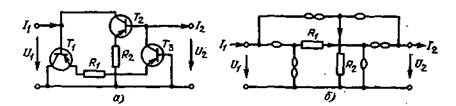
НУЛЛАТОР (рис. 3.19,а) является двухполюсником, который обращает в нуль протекающий через него ток и приложенное к нему напряжение: I=0; U=0. НОРАТОР (рис. 3.19, б) является двухполюсником, ток и напряжение ко­торого принимают любые, не связанные между собой значения: I — любое; U—любое. Нуллатор и норатор нельзя описать с помощью закона Ома [17]. Последовательное соединение нуллатора и норатора эквивалентно разрыву вет­ви (холостому ходу) (рис. 3.20,а), а параллельное соединение –

короткозамкнутой ветви (короткому замыканию) (рис. 3.20, б).

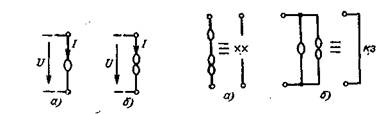
Рис. 3.19                                                    Рис. 3.20

НУЛЛОР является четырехполюсником (рис. 3.21), у которого входные ток и напряжение равны нулю, а выходные ток и напряжение принимают любые, не связанные между собой значения. На рис. 3.21, а изображен неуравновешенный, а на рис. 3.21, в - уравновешенный нуллор. Нуллор можно представить состоя­щим из нуллатора и норатора (рис. 3.21, б, г), поэтому пара «нуллатор — нора­тор» эквивалентна нуллору (или является его схемой замещения).

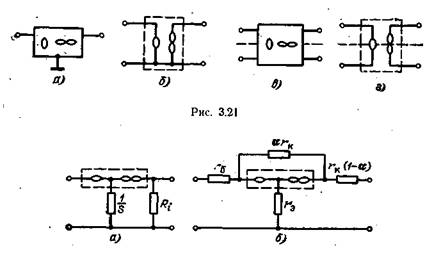
Рис. 3.22

 

На рис. 3.22, а, б изображены соответственно эквивалентные схемы трехэлектродной лампы и полупроводникового триода. Схемы содержат нуллор. Из анализа этих схем следует, что нуллор эквивалентен высококачественному ламповому триоду, у которого l/S→0, R_i→∞, либо высококачественному полу­проводниковому триоду, у которого (1- α)r_k→0, r_б→0, r_э→0, r_k→∞ где S — крутизна; R_i — внутреннее сопротивление триода; r_k, r_б, r_э — сопротивле­ния базы, эмиттера и коллектора транзистора; α — коэффициент, равный отно­шению токов коллектора и эмиттера (при r_k→∞).

Сравнение нуллора с недифференциальным операционным усилителем (ОУ) показывает, что нуллор эквивалентен идеальному ОУ, так как у идеального ОУ согласно (ЗЛ'З) входной ток и входное напряжение равны нулю (при ко­нечном выходном напряжении), а выходной ток и напряжение—любые (усиле­ние усилителя равно ∞, |μ|->оо). Таким образом, заземленный нуллор можно отобразить одним из трех высококачественных элементов: транзистором, лам­повым триодом и операционным усилителем (рис. 3.23,а). База (б) и сетка (с) соответствуют зажиму / нуллора, коллектор (к) и анод (а) — зажиму 2, эмит­тер (э) н катод (к) — зажиму 3. Нуллор с заземленным выходом отображает ДОУ (рис. 3.23,6), а уравновешенный нуллор отображает уравновешенный ДОУ (рис. 3.23, в).

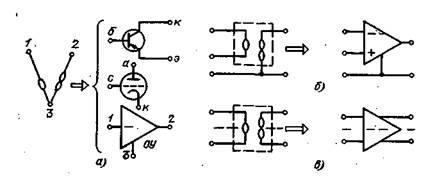
Рис. 3.23

Наряду с иуллатором используется также более общий аномальный эле­мент: бигенератор (двойной генератор) — двухполюсник, задающий ток I₀ и задающее напряжение U₀ которого фиксированы: I₀ = const, U₀ =const (в част­ности, ток и напряжение могут обращаться в нуль). Если I₀ = U₀ = 0, то биге­нератор вырождается в иуллатор. Бигенератор можно отобразить с помощью иуллатора, источника напряжения U₀ и источника тока I₀, как указано на рис. 3.24.

Включение аномальных элементов в цепь может привести к нарушению за­конов и правил теории электрических цепей и появлению цепей с неопределен­ным состоянием. Примеры таких нарушений:

1. На рис. 3.25 изображена цепь, в которой состояние ветви 1 не определено, а в ветви 2 нарушаются законы Ома и Кирхгофа.

 

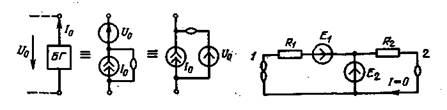
Рис. 3.24                                                    Рис. 3.25

2.  Если в цепи выбрать произвольный двухполюсник, подчиняющийся закону Ома, то режим работы цепи не нарушится при замене двухполюсника источ­ником напряжения,  создающим то же напряжение, что и на двухполюснике, либо источником тока, задающий ток которого равен току двухполюсника. Эти замены не применимы к нуллатору.

3.  Известно, что режим работы цепи не нарушится, если соединить между собой эквипотенциальные ее точки и разорвать ветви с нулевыми токами. Это правило не применимо к нуллатору: нельзя закорачивать нуллатор, хотя его зажимы являются эквипотенциальными точками, и разрывать ветвь с нуллато­ром, хотя его ток равен нулю.

4. Цепь без источников, составленная из произвольных двухполюсников, подчиняющихся закону Ома, удовлетворяет принципу взаимности (обратимости). Если же в цепи есть аномальные элементы, то в общем случае она является невзаимной.

Уравнения равновесия произвольной многополюсной цепи, в которую включены аномальные элементы  (рис. 3.26), записываются согласно правилам:

1. Удалить из цепи все аномальные элементы (разорвать и удалить ветви с нуллаторами, иораторами и бигеиераторами). Для оставшейся регулярной части цепи записать уравнения (3.5) обычными методами.

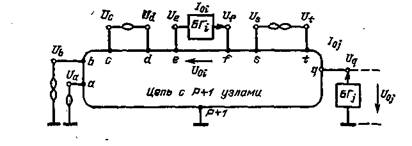
Рис. 3.26

 

2.  Включить в цепь аномальные элементы. В записанной системе (3.5) урав­нять между собой напряжения узлов, между которыми включены нуллаторы, и учесть, что напряжения узлов, между которыми включены бигенераторы, от­личаются иа задающие напряжения бигенераторов. В результате этого умень­шится число неизвестных напряжений на суммарное число нуллаторов и биге­нераторов. Например, в цепи рис 3.26 необходимо положить U_с=U_d; U_a = 0 (узел а связан нуллатором с базисным узлом, напряжение которого равно нулю); U_f=U_e+ U_0i; U_q = U_0j; U_0i, U_0j — задающие напряжения (ЭДС) i-го и j-го бигенераторов.

3.  К правым частям уравнений (3.5), т. е. к задающим токам I_rk узлов, между которыми включены бигеиератрры, прибавить либо вычесть задающие токи бигенераторов (в зависимости от направлений токов бигенераторов). На­пример, в цепи рис. 3.26 необходимо /0« прибавить к току Iff и вычесть /щ из тока /„; к току /„ необходимо прибавить /0,- (здесь /0<, los — задающие токи бигенераторов).

4.  Просуммировать уравнения узлов, между которыми включены нораторы. Отбросить уравнения узлов, которые соединены с базисным узлом норатором. Это уменьшит число уравнений на число иораторов. Например, для цепи рис. 3.26 необходимо к уравнению узла t прибавить уравнение узла s и отбросить уравнение узла Ь.

Если число нуллаторов и бигенераторов равно числу нораторов, то в ре­зультате проделанных преобразований уравнеиий (3.5) приходим к системе уравнений, в которой число неизвестных напряжений равно числу уравнеиий. Далее, если определитель полученной системы уравнеиий не равен нулю, то состояние цепн (напряжения узлов цепи) находится решением уравнений обыч­ными методами.

 

 

I
\y0 + yx    — yx
— Yx    YX + KY    —KY
\                  —KY     KY+Y			— Y
\    -Y			— Y
1               1
Y0 + Yx\    -Yx
KY+Y\ —KY	— Y

В этой матрице прибавим к столбцу 1 столбцы 2 н 4, удалим столбцы 2 н 4, вычеркнем строки 3 и 5. В результате получим матрицу проводнмостей всей цепи

1+2+4        3               5

2 4

По матрице Y согласно (3.7) найдем

Расчет простых цепей, содержащих аномальные элементы, в некоторых слу­чаях удобно проводить, используя непосредственно законы Ома и Кирхгофа. Аномальные элементы не описываются законом Ома. Однако цепи, содержа­щие аномальные элементы, естественно, удовлетворяют основным законам элек­трических цепей, т. е. законам Кирхгофа:

1.   Первый закон Кирхгофа (закон токов) — алгебраическая сумма токов любого  узла   (в общем  случае — сечения)   электрической  цепн равна  нулю.

2.   Второй закон Кирхгофа (закон напряжений) — алгебраическая сумма напряжений любого замкнутого контура электрической цепн равна нулю.

Приведем   пример,   иллюстрирующий   непосредственное  применение  законов Кирхгофа при расчете цепей с аномальными элементами. Пример. Найти входное сопротивление цепн рнс. 3.28,а.

Допустим, что цепь рис. 3.26 не содержит источников и бигенераторов, ио имеет нуллаторы и нораторы. Матрица проводнмостей такой цепи Y формиру­ется по правилам:

1.   Удалить из цепи все аномальные элементы. Записать матрицу проводн­мостей Y₀ регулярной части цепи.

2.   Включить в цепь аномальные элементы. Просуммировать между собой попарно столбцы матрицы Y₀, соответствующие узлам, между которыми включены нуллаторы. Вычеркнуть столбцы, соответствующие узлам, соединенным с базис­ным узлом нуллаторами.

3.   Просуммировать между собой попарно строки матрицы Yo, соответст­вующие узлам, между которыми включены нораторы. Вычеркнуть строки, со­ответствующие узлам, соединенным с базисным узлом норатором.

В результате проделанных преобразований приходим к матрице Y. Функции цепн с аномальными элементами находятся по матрице Y так же, как и функ­ции цепи с МОУ, т. е. по (3.7)—(3.9).

Пример. Найти передаточную функцию по напряжению цепи рис. 3.27,а. На рис. 3.27,6 изображена цепь после замены ДОУ нуллорами. Матрица про­воднмостей регулярной части цепн

12                 3                 4                 5

1 2

4 5

Рис. 3.28

Как уже указывалось, высококачественные транзисторы н ламповые триоды можно заменить нуллорамн (см. рнс. 3.23,а). Для низкокачественных транзи­сторов и триодов такая замена, естественно, является приближенной. Тем не менее она используется для приближенной оценки свойств сложных схем, со­держащих большое число транзисторов нлн триодов, поскольку расчет схем с нуллорамн проще расчета схем   с реальными транзисторами и триодами.

Рис. 3.39

Замена операпнонных усилителей нуллорамн приводит к цепи рнс. 3.28,6. Очевидно, что (напряжения нуллаторов равны нулю). Поскольку токи

иуллаторов равны нулю, через двухполюсник  поотекает ток, через двух­полюсники— ток /'г, через двухполюсники— ток h.

Уравнения контуров /н 11:

Из этих  уравненийполучим  li=hZiZ₃/ZzZi..  Входное сопротивление цепи

Рис. 3.30

2.   Источник иапряжеиня, управляемый током (рис. 3.30,6), Е=ц/₀ь, где ц — коэффициент  пропорциональности  с   размерностью  сопротивления.

3.   Источник тока, управляемый напряжением (рис. З.ЗО.в), /=ц(/_аь, где \i — коэффициент   пропорциональности   с   размерностью   проводимости.

4.   Источник тока, управляемый током (рис. З.ЗО.г),/=ц/₀ь, где ц — без­размерный коэффициент пропорциональности. Во всех источниках ц — произ­вольный коэффициент,  т.  е.  вещественный,  комплексный  нлн операторный.

Все зависимые источники — четырехполюсники. Зависимые источники явля­ются односторонними преобразователями, преобразующими управляющие токи и напряжения в задающие токи и напряжения источников. Так, источник рис. 3.29,а — преобразователь напряжения в напряжение (сокращенно — ПНН), источник рис. 3.30,6 — преобразователь тока в напряжение (ПТН), источник рис. З.'30,в — преобразователь напряжения в ток (ПНТ), источник рис. З.ЗО.г — преобразователь тока в ток (ПТТ). Зависимые источники—это предельно прос­тые МОУ с одним входом и одним выходом, поэтому цепи, содержащие за­висимые источники, рассчитываются так же, как и цепи с МОУ, при условии, что один нз зажимов зависимых источников н одна из точек цепи управления (точка а или Ь) соединены с базисным узлом цепи.

Общие правила расчета многополюсных цепей с зависимыми источниками следующие.

цепь с источником напряжения, управляемым напряжением (рис. 3.31,а). Уравнение    зависимого    источника   E—V_c—Ј/d = n(Ј/a—Ub),   откуда   £/ь = (/<,+

+ —Ud——Uc* где  U_a,  Ub,  Uc,  Ud — напряжения узлов  a,  b, с, d относн-

ц            ц

тельно базисного [(Р-Н)-го] узла.

Удалим нз цепн зависимый источник (разорвем ветвь с ЭДС Е) и для ос-ставшейся регулярной части цепи запишем уравнения по методу узловых на­пряжений (3.5). Включим в цепь зависимый источник и запишем ее уравнения в форме (3.6). Переход от Y₀ к Y произведем по правилам рис. 3.31,6:

Пример. Записать в общем виде приближенную связь между токами н на­пряжениями на входе н выходе цепн рис. 3.29,а. Заменив в первом приближе­нии транзисторы Ti—Тз нуллорамн, придем к схеме рнс. 3.29,6. Учитывая, что токи всех нуллаторов равны нулю, нетрудно видеть, что через резистор Ri про­текает ток /₂, а через резистор R₂ — ток h. Далее, учитывая, что напряжения иуллаторов равны нулю, нетрудно видеть, что напряжение на резисторе Ri равно 0\, а на резисторе #2 — U₂, поэтому Ui=IiRu Ui^hRz, h^UzIRi, h=* ^Ui/Rf. Полученные выражения показывают, что цепь рис. 3.29,а является ин­вертором сопротивления, в частности гнратором, если Ri=R2  (см.  [17]).

Зависимые источники

Зависимые (управляемые) источники тока и напряжения — это источники, задающие токи или ЭДС (задающие напряжения) которых линейно зависят от некоторых управляющих токов и напряжений. Известны четыре вида зависи­мых источников:

1. Источник напряжения, управляемый напряжением, — это источник, ЭДС которого Е прямо пропорциональна управляющему напряжению (/<,&, прило­женному к некоторым точкам а, Ь цепн, в которую источник включен (рис. 3.30,a): E=\iU_ab, где ц— безразмерный коэффициент пропорциональности.